GENERALITES SUR LES FONCTIONS

 

GRAPHE d’une FONCTION

 

On dote le plan d’un repère orthonormé.    Soit une fonction, y = f(x). 

Le graphe de f(x) est l’image dans ce repère des points de coordonnées (x, f(x)) .

Pour avoir un point du graphe, il suffit de donner une valeur à x et de calculer y =f(x). On trace le point dans le plan, puis on change de valeur de x et on obtient un autre point. Ainsi de suite… 

En général, on obtient une courbe qui nous renseigne sur la façon dont f(x) se comporte selon les valeurs de x .

Le but d’une étude de fonction est, en principe de tracer son graphe et d’étudier quelques comportements particuliers.

Voici le graphe des fonctions les plus courantes que vous devez connaître..

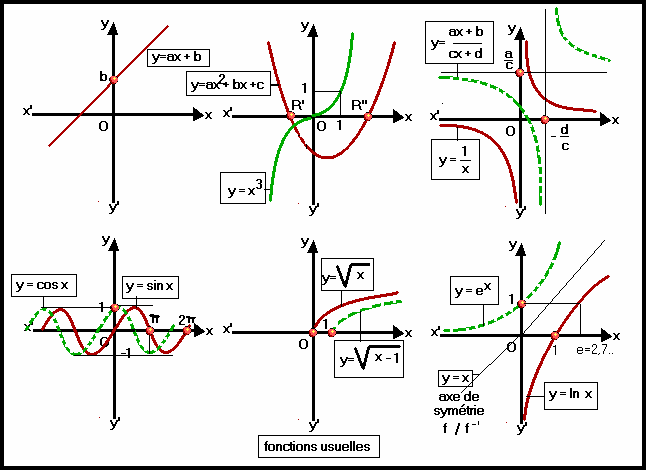
A ce stade on doit savoir que

l les points du graphe qui sont sur l’axe de x vérifient y =  0 . Pour  trouver leur abscisse, il faut résoudre f(x) = 0.

l les points du graphe qui sont sur l’axe des y vérifient x = 0.  Pour trouver leur ordonnée, il suffit d’écrire y = f(0).

 

Remarque :

Le graphe d’une fonction est en général assimilé à son image dans un plan, mais il ne faut pas perdre de vue

● que les axes sont en réalité deux images du même ensemble R

● que le plan est en réalité une image de R2. Chaque point  du plan est associé au couple (x, y ) de ses coordonnées et (x, y ) est bien un élément de R2.

Ainsi la définition mathématique du graphe est la suivante :

 

Le graphe d’une fonction f est l’ensemble des couples (x,y) de R2 , tels que y = f(x)

G f  = { (x,y) ∈ R2  | y = f(x) } .

 

Pour une application f de E dans F , on définirait ainsi le graphe  G = { (x,y) ∈ E X F  | y = f(x) }

 

Dans le plan rapporté à un système de coordonnées (on choisit un repère orthonormé pour que la notion de distance ou de mesure dans le plan et sur les axes ait un sens) , les points qui forment G f  tracent un dessin, généralement on dit « une courbe », et comme cette courbe est bien l’ensemble des points (x,y) appartenant au graphe, il est judicieux de faire l’amalgame entre la courbe et le graphe. 

Quand on définit des distances, dans le plan et sur les axes, ces définition vont porter sur R ou sur R2 , et elles seront cohérentes avec les distances « intuitives » mesurées sur le dessin .

 

 

Domaine de définition

 

Certaines fonctions ne sont pas définies pour toutes les valeurs de x . Notamment :

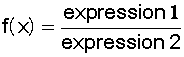●  n’est pas définie pour (expression 2 = 0)  (le dénominateur ne peut être nul)

 

On va donc résoudre l’équation expression 2 = 0 et trouver les valeurs (x = A , x = B, ….) qui annulent expression 2.

Puis on dira que le domaine de définition de f(x) est R privé de A , B , …           Df  = R / { A ; B ; ….}

 

●  n’est pas définie pour expression 1 négative. (la racine d’un nombre négatif n’existe pas) .

On va donc résoudre l’inéquation expression 1 ≥ 0 , la solution étant un intervalle Is de R, et dire  Df = Is .

 

● Si f(x) combine des racines et des dénominateurs, on exclura de Df tout ce qui doit l’être .

 

● l’étude des graphes de fonctions usuelles montre que   f(x) =ax2+bx+c est définie pour tout x ∈R  (Df = R)

f(x) =   a pour Df : R / {0} ➜ discontinuité du graphe en x =0.  

 

f(x) = 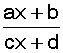 a pour Df   R / {}  ➜ discontinuité du graphe en x = –d/c

 

f(x) =   a pour Df   l’intervalle [ 0 , + ∞ )  ➜  absence de graphe sur (–∞ , 0 [

 

f(x) =  a pour Df  l’intervalle   [ 1 , +∞ ) ➜ absence de graphe sur (–∞ , 1 [

 

Ces cas sont les plus connus, mais il faut savoir par exemple :

● que la fonction ln x n’est définie que pour x ∈ R + *  à valeurs dans R

● que la fonction ex est définie pour x ∈ R à valeurs dans R + *

● que la fonction arc sin x  est définie sur [ –1 , + 1]  à valeurs dans [ –π/2 , + π/2]

● que la fonction arc cos x  est définie sur [ –1 , + 1]  à valeurs dans [ –π , + π]

● que la fonction arc tan x  est définie sur  R  à valeurs dans [ –π/2 , + π/2]

 

 

FONCTION DEFINIE PAR MORCEAUX (valeur absolue d’une expression en x)

 

C’est une fonction dont la définition ou l’écriture change sur certains intervalles de son domaine de définition.

C’est en général le cas des fonctions contenant la valeur absolue d’une expression en x .

Au préalable rappelons qu’on peut écrire  = 3 mais = |x| ou plus généralement = |g(x)|.

En effet , la racine de x2 (et plus généralement de (g(x))2 ) est définie quel que soit x puisqu’un carré est toujours positif,  mais en extrayant la racine, on doit, par définition obtenir un nombre positif . C’est pourquoi ce qu’on extrait de la racine doit être désigné comme une valeur absolue, qui elle reste positive quelle que soit la valeur donnée à x.

Comment se comporte f(x) = |x| ? Cette expression est définie quel que soit x mais …

si x est négatif (x ∈ (–∞ ; 0] )      ➜  |x| = –x      ➜  f(x) = –x

si x est positif  (x∈ [0 ; + ∞ ) )      ➜ |x| = + x     ➜  f(x) = x

C’est donc typiquement une fonction définie par morceaux .

Plus généralement si f(x) intègre une expression de type |g(x)| :

On va étudier le signe de g(x) et trouver  g(x) ≥ 0 sur un intervalle I+  et g(x)≤ 0 sur un intervalle I– .

Puis sur I+ , on remplacera |g(x)| par g(x)  et sur I– ,  on remplacera |g(x)| par –g(x) dans l’expression de f( x ).

Exemple :

Comportement de f(x) =  ?

La fonction est définie pour tout x ∈R .  Df = R .

On écrit que f(x) = |x+1| .

Si  x +1 > 0  soit x  > –1 , on a f(x) = x + 1

Si  x +1 < 0 soit   x  < – 1 , on a  f(x) = –(x+1) = –x – 1 .

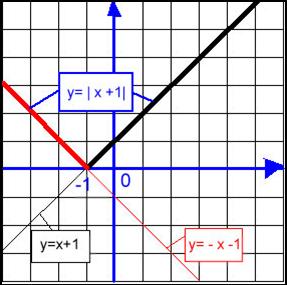
En bleu le graphe de f(x) qui est composé de deux morceaux :

Sur (–∞ ; –1] , une fonction qui coïncide avec la droite  y = –x – 1

Sur [ –1 ; + ∞) une fonction qui coïncide avec la droite y = x+ 1 .

 

C’est comme si la fonction « rebondissait » au moment où elle allait devenir négative pour rester dans le demi plan où y est positif  . Ce comportement est imposé par la racine, ou la valeur absolue,  contenue dans sa définition.

 

 

 

 

 

 

Pour définir une fonction par morceaux, il suffit de faire une partition de R en intervalles qui ne se chevauchent pas

(Par définition dans une partition les ensembles sont disjoints et leur réunion est l’ensemble partitionné)

Par exemple ( – ∞ , a [ ,  [a , b[  , [ b , + ∞ ) et définir R comme on veut sur chaque intervalle 

Sur  ( – ∞ , a [ on aura f(x) = g(x)  , sur  [a , b[ on aura f(x) = h(x) , sur [ b , + ∞ ) on aura f(x) = i(x) .

Si g , h , i sont définies sur chacun des intervalles qui leur est attribué, alors f est définie sur R .

 

 

 

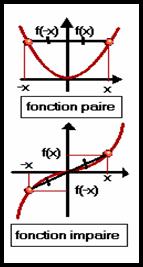
FONCTION PAIRE / FONCTION IMPAIRE

 

● Quand une fonction est paire , son graphe est symétrique par rapport à l'axe des y.

Par exemple y = cos x  et y =x2 sont des fonctions paires .

● Quand une fonction est impaire, son graphe est symétrique par rapport à l'origine (O) .

Par exemple y = sin x ,  y = x3 et y =  sont des fonctions impaires .

 

Dans les 2 cas , on peut donc restreindre l'étude de f(x) à la moitié positive de Df .

 

 

Comment les repérer ?

Il faut d'abord que pour tout x appartenant à Df , (-x) appartienne à Df .

Ensuite ...

● une fonction est paire si pour tout x appartenant à Df on a f(-x) = f(x)

Par exemple : cos(-x) = cos(x) ,  (-x)2 = (x)2  .

● une fonction est impaire si pour tout x appartenant à Df on a f(-x) = - f(x).

 

 

Par exemple             sin(-x) = - sin(x)  ,               (-x)3 = -(x)3 ,                      

 

 

 

 

 

FONCTION PERIODIQUE

 

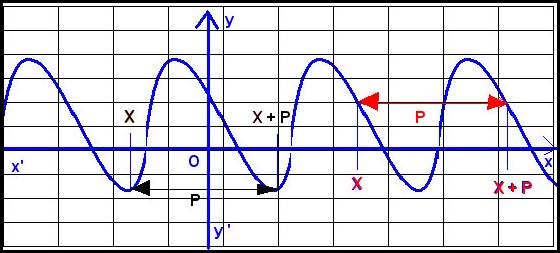
Une fonction est dite périodique sur R si il existe un nombre P (appelé période) tel que pour tout x ∈ R , f(x) = f(x +P)

 

Si la fonction est périodique, il suffit de restreindre son étude à une période [ a , a + P ] et on déduira son graphe de l’étude faite sur ce « morceau » par translation le long de l’axe des X.

 

 

 

 

 

GRAPHE DE LA FONCTION  RECIPROQUE

 

Si y = f(x) une fonction bijective elle admet une fonction réciproque f–1 et à chaque point (x,y) du graphe de f (tel que y = f(x)) , il correspond un point (y,x) du graphe de f–1 (tel que x = f–1 (y)) .

Or les points (x , y) et ( y ,x) sont symétriques par rapport à la bissectrice principale des axes qui est la droite d’équation y = x . .

Conclusion :

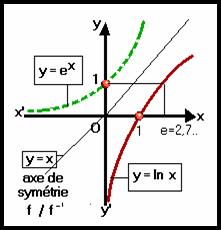
Les graphes de la fonction et de sa fonction réciproque sont symétriques par rapport à la droite d’équation

y  = x.

 

On l’observe, ci contre dans la représentation des graphes de ln x et ex qui sont réciproques l’une de l’autre puisque si y = ln x on a x = e y .

Cela peut nous aider dans l’étude de la fonction réciproque d’une fonction connue.

 

 

 

Au fait : Quelle est l’équation de la droite symétrique de la droite d’équation y = 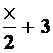 par rapport à la droite y = x ?

C’est simple, c’est la fonction réciproque de x ➜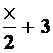 . De y =  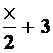on tire x = 2y – 6 donc, la droite cherchée est la droite d’équation y = 2x – 6 .

 

Remarque : quand f –1 = f , comme c’est le cas pour f : x ➜  , le graphe de f est symétrique par rapport à la droite d’équation y = x .

 

 

 

 

 

CHANGEMENTS DE REPERES ET DE VARIABLES

 

 

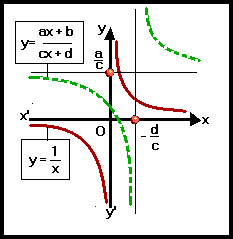
Sur ce dessin, on voit

(en vert) le graphe de 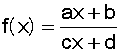 et (en rouge) celui de

 

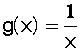
Les 2 graphes se ressemblent furieusement  sauf qu’ils n’ont pas les mêmes asymptotes. Pour  g(x) ce sont les axes du repère, pour f(x) les droites d’équation x = – d/c et y = a/c.

Notre but est de trouver l’équation de f(x) en prenant ses asymptotes pour axes. 

P, le point d’intersection des asymptotes de f(x) a pour coordonnées ( - d/c , a/c). Ce sera l’origine du nouveau repère.

 

 

 

 

On passe du repère (O , i , j) au repère (P, i, j) 

Dans ce type de changement de repère,

si les coordonnées d’un point  dans le repère (O , i , j) sont (x,y) ,

ses nouvelles coordonnées dans le repère (P , i , j) seront  (X = x – a , Y = y – b) ,

a et b étant les coordonnées de la nouvelle origine.

Ce qui dans notre cas donne X = x + d/c et Y = y – a/c .

On a donc x = X – d/c et y = Y + a/c .

 

En remplaçant x et y par leur valeur dans l’expression de f(x) ; on trouve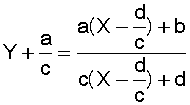  

 

Après simplification, au dénominateur du second membre il ne reste que cX.

Quand on va isoler Y dans le premier membre et réduire le second membre après réduction au même dénominateur les X du numérateur vont s’annuler si bien qu’on va avoir un résultat de la forme

 

  Y= K

 

 

K étant un réel non nul  fonction de a, b, c, d. La nouvelle formulation de f(x) est déjà plus facile à étudier.

Selon la valeur de K (< 1 ou > 1) le graphe de f(x) sera plus « écrasé » sur l’axe des x ou au contraire plus « éloigné » de cet axe que le graphe de . Pour corriger ce défaut, il suffit de faire un nouveau changement de variable soit

Y = Ky  soit  X = Kx ce qui revient à prendre pour repère soit (P , i , ) soit (P , , j) (non orthonormés) . 

Finalement, dans ce dernier repère l’équation de f(x) devient y = .

 

Changements de repères

On peut imaginer toutes sortes de changements de repères.

Le plus fréquemment employés sont ceux du type ( O , i , j ) → ( P , i , j ) où les axes résultants sont des translatés des axes d’origine. Ils sont utiles pour montrer

● soit la symétrie d’un graphe par rapport à un point P (dans le nouveau repère la fonction devient impaire)

● Soit la symétrie d’un graphe par rapport à un axe (dans le nouveau repère la fonction devient paire)

ce qui facilite l’étude de la fonction.

Les changements de variables correspondant à ce changement de repère sont :

 

Changement d’origine , mêmes vecteurs unitaires

( O , i , j ) → ( P , i , j )

 

●  si P (nouvelle origine)  a pour coordonnées (a , b)

● Si (x , y)  sont les anciennes coordonnées d’un point

et (X , Y) les nouvelles

On a

X = x – a

Y = y –b

 

 

Autre changement de repère, moins fréquent parce qu’il pervertit les distances dans le plan

Changement d’unité sur un axe

( O , i , j ) → ( O ,  , j )

 

● Si (x , y)  sont les anciennes coordonnées d’un point

et (X , Y) les nouvelles

On a

X = Kx

 

 

On peut imaginer d’autres changements, plus difficiles à mettre en œuvre : Par exemple, faire tourner les vecteurs i et j d’un angle θ, ce qui revient à mettre en œuvre une rotation d’angle – θ, du vecteur OM .

 

Fonctions composées

On les reconnaît souvent à ce qu’on obtient une fonction usuelle par un changement de variable.

Par exemple, dans f : x → sin 2 x , il suffit de faire X = sin x  pour reconnaître la fonction g : X → X2 .

Si on pose h : x → sin x  on a alors f = g ○ h   de qui équivaut à  

f(x) = g(h(x)) = (h(x)) 2 = (sin x )2 = sin 2 x